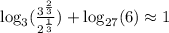
1) Let's simplify this logarithm expression, making use of properties.
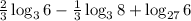
2) Let's rewrite that expression turning the factor 2/3 back into an exponent
as well as that -1/3:
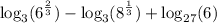
Now, let's rewrite that difference into a quotient:
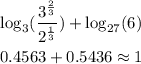
Since the question does not allow the use of calculator, then we can leave it as the simplest possible expression. Although, the answer is approximately 1.