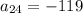We have here in this an arithmetic progression. We have that the common difference is d = -5. (If we add -5 to -4, we obtain the second term -9, and so on).
We have that the first term is -4.
Then, according to the equation for the arithmetic progressions, we have:

Then, the equation to find the nth term is the one above.
The equation for this case is:
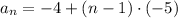
For example, we have in the sequence that the fourth term is -19. Then:
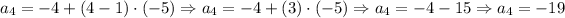
Therefore, to find the 24th element of the arithmetic progression, we have:
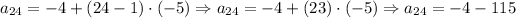
Then, the 24th element is: