Question

The area of a rectangle is 54x y9 3 6x y4 yards, 8 square yards. If the length of the rectangle is which expression represents the width of the rectangle in yards?Answers:9x¹²y¹²9x⁶y⁴324x¹²y¹²324x⁶y⁴

Answer 1

9x⁶y⁴

Step-by-step explanation:

The area of a rectangle is equal to:

`\text{Area }=\text{ Length x Width }`

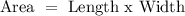
So, dividend both sides by the length, we get that the width can be calculated as:

`\text{Width = }\frac{\text{ Area}}{\text{ Length}}`

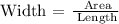
Then, replacing the expression for the Area and the length, we get:

`\text{Width = }(54x^9y^8)/(6x^3y^4)`

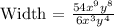
Now, we will use the following property:

`(a^m)/(a^n)=a^(m-n)`

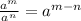
It means that when we divide two numbers with the same base, we subtract the exponents. So, the width is equal to:

`\begin{gathered} \text{Width}=(54)/(6)\cdot(x^9)/(x^3)\cdot(y^8)/(y^4) \\ \text{Width}=9\cdot x^(9-3)\cdot y^(8-4) \\ \text{Width}=9x^6y^4 \end{gathered}`

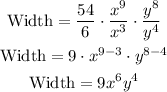
Therefore, the expression that represents the width of the rectangle in yards is: 9x⁶y⁴