Question

A. find an equation for f(t) B. explain how you can use the graph's t-intercept to check the reasonableness of your equation.

Answer 1

the form of a parabola has the form

`f(t)=at^2+bt+c`

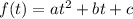
when t=0

`f(0)=c`

usinc the graphic when t = 0 the value on the y axis is 45

`c=45`

now using the formula for the vertex:

`\begin{gathered} \text{vertex}=(h,k) \\ h=(-(b)/(2a));k=f(-(b)/(2a)) \\ \end{gathered}`

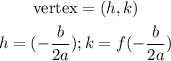
since h=0

`0=-(b)/(2a)\rightarrow b=0`

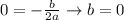
the only possible way for this to be 0 is if the numerator is equal to 0, reason why b is 0

now using the point given, we find a

`\begin{gathered} y=at^2+c \\ 29=a+45 \\ 29-45=a \\ a=-16 \end{gathered}`

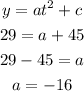
re write the equation

`f(t)=-16x^2+45`

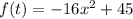
there is not h, inside the parentheses beacuse h=0

Does the equation makes sense?

Yes, because the number accompanying the x^2 the parabola is upside-down, also the vertex its on (0,45) menaing the parabola moved 45 units up.

Also since the hammer is dropping the y should become less ultil it gets to the floor.