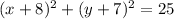We have two points describing the diameter of a circumference, these are:
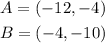
Recall that the equation for the standard form of a circle is:
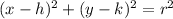
Where (h,k) is the coordinate of the center of the circle, to find this coordinate, we find the midpoint of the diameter, that is, the midpoint between points A and B.
For this we use the following equation:
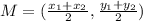
Now, we replace and solve:
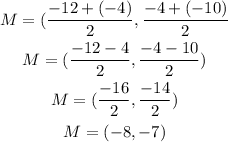
The center of the circle is (-8,-7), so:
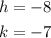
On the other hand, we must find the radius of the circle, remember that the radius of a circle goes from the center of the circumference to a point on its arc, for this we use the following equation:
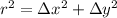
In this case, we will solve the delta with the center coordinate and the B coordinate.
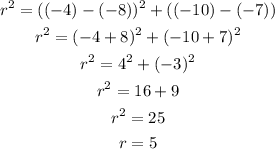
Therefore, the equation for the standard form of a circle is:
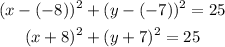
In conclusion, the equation is the following: