ANSWER
85.9° North of East
Step-by-step explanation
First, we have to make a sketch:
We have to find the resultant vector of the car's displacement.
The horizontal component of the displacement of the car:
![\begin{gathered} d_x=-10\cos 45+15\cos 60 \\ d_x=(-10\cdot0.7071)+(15\cdot0.5)=-7.071+7.5 \\ d_x=0.429\operatorname{km} \end{gathered}]()
The vertical component of the displacement of the car is:
![\begin{gathered} d_y=-10\sin 45+15\sin 60 \\ d_y=(-10\cdot0.7071)+_{}(15\cdot0.8660)=-7.071+12.990 \\ d_y=5.919\operatorname{km} \end{gathered}]()
To find the direction of the car's resultant vector, apply the formula:
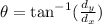
Therefore, we have:
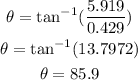
Hence, the car's resultant vector is 85.9° North of East.