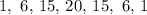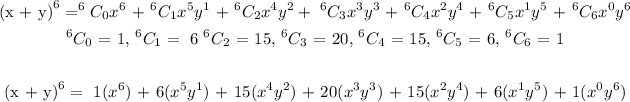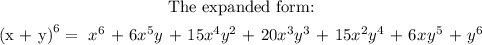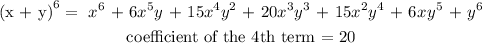
Step-by-step explanation:
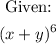
To expand the above, we will use the binomial theorem and pascal's triangle
Using binomial theorem expansion:
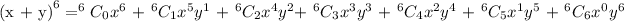
The values of the combination can be gotten from pascal's triangle. Pascals triangle gives the coefficient of each term
The exponent is 6, we will find the coefficient when the exponent is 6: