Question

Find the sum of the first 10 terms of the following geometric sequences:(1.5, 3, 6, 12, 24...}

Answer 1

Okay, here we have this:

Considering the provided geometric sequence, we are going to calculate the sum of the first 10 terms, so we obtain the following:

Then we will substitute in the following formula the Sum of the First n Terms of a Geometric Sequence:

Let us remember that in our case "r" is equal to 2, because each term is equal to the previous one multiplied by 2, we have:

`S_n=(a_1(1-r^n))/(1-r)`
`\begin{gathered} S_(10)=(1.5(1-2^(10)))/(1-2) \\ S_(10)=(1.5(1-1024))/(-1) \\ S_(10)=-1.5(-1023) \\ S_(10)=1534.5 \end{gathered}`

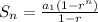
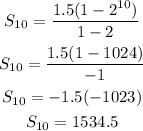
Finally we obtain that the sum of the first 10 terms of the geometric sequence is equal to 1534.5.