Question

A student government class has 20 students. Four students will be chosen at random to represent the school ata city council meeting.

Answer 1

This is a case of combination. This is because for this case the order has no importance. Let's say students A, B, C and D were chosen for the group of 4. To choose first A, then C, D and B will gives us exactly the same group obtained of we first select student C, then B, A and D.

To solve it we can simply use the formula for combination:

`\text{nCx=}(n!)/(x!(n-x)!)`

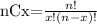
For this case n is 20 (the number o students) and x is 4 (the number of representatives):

`\begin{gathered} 20C4=(20!)/(4!\cdot(20-4)!) \\ 20C4=(20!)/(4!\cdot16!) \end{gathered}`

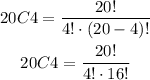
20! is 20x19x18x17x16x15 and so on. We can represent it in a convenient way as: 20! = 20x19x18x17x16!:

`20C4=(20\cdot19\cdot18\cdot17\cdot16!)/(4!\cdot16!)`

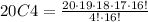
Then, the 16! in the numerator can be simplified with the 16! in the denominator:

`\begin{gathered} 20C4=(20\cdot19\cdot18\cdot17)/(4!) \\ 20C4=(20\cdot19\cdot18\cdot17)/(4\cdot3\cdot2\cdot1) \\ 20C4=(116280)/(24)=4845 \end{gathered}`

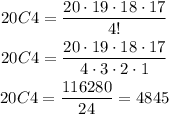
There are 4845 different ways to choose a group of 4 among 20 people.