Question

Please assist me in answering number 3. I would appreciate you helping me with detailed reasons on how you calculated the answer. Thank you for your help and patience

Answer 1

Question 3.

Given the equation:

`C(t)=9(0.5)^(0.021t)`

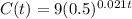
Where C is in milligrams per litre t minutes after taking the medicine.

Let's solve for the follosing:

• (a). Write down C(0).

To find C(0), substitute 0 for t and solve for c(0):

`\begin{gathered} c(0)=9(0.5)^(0.021*0) \\ \\ c(0)=9(0.5)^0 \\ \\ c(0)=9(1) \\ \\ c(0)=9 \end{gathered}`

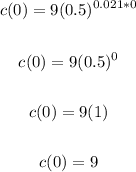
• (b). Find the concentration of the medication left in the patient's bloodstream after 40 minutes.

Substitute 40 for t and solve for C(40).

We have:

`\begin{gathered} c(40)=9(0.5)^(0.021(40)) \\ \\ c(40)=9(0.5)^(0.84) \end{gathered}`

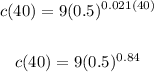
Solving further:

`C(40)=5.02\text{ mg}`

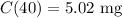
Therefore, the concentration after 40 minutes is 5.03 milligrams per litre

• (c)., To solve this, first substitute 0.350 for C(t) and find t:

`\begin{gathered} 0.350=9(0.5)^(0.021t) \\ \\ \end{gathered}`

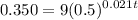
Divide both sides by 9:

`\begin{gathered} (0.350)/(9)=(9(0.5)^(0.021t))/(9) \\ \\ (0.350)/(9)=0.5^(0.021t) \end{gathered}`

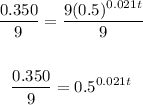
Take the natural loagraithm of both sides:

`\begin{gathered} ln((350)/(9))=0.021tln(0.5) \\ \\ −3.247046=0.021t(−0.693147) \\ \\ −3.247046=-0.014556t \\ \\ t=(−3.247046)/(-0.014556) \\ \\ t=223.07 \end{gathered}`

Therefore, the patient will take the medicine again 223 minutes after 14:00.

Convert the time to hours:

Where 60 mins = 1 hour

`(223)/(60)=3\text{ hrs 43 mins}`

14:00 + 3:43 = 17:43

Therefore, the patient will take the medicine at 17:43

ANSWER:

(A). 9

(B). 5.02 mg per litre

(c). 17:43