Question

Please check the photo (Calculus), I just need the first part of this answer solved.

Answer 1

The given function is

`f(x)=15-x^2^{}`

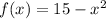
First, we have to find f(x+h), which consists of adding h to the x-variable.

`f(x+h)=15-(x+h)^2`

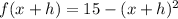
Then, we use the functions we have in the slope definition.

`\lim _(h\to0)((f(x+h)-f(x))/(h))=\lim _(h\to0)((15-(x+h)^2-(15-x^2))/(h))`

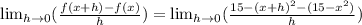
Solve the notable product and multiply by the negative sign in front.

`\lim _(h\to0)((15-(x^2+2xh+h^2)-15+x^2)/(h))=\lim _(h\to0)((15-x^2-2xh-h^2-15+x^2)/(h))`

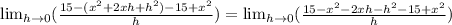
Add like terms.

`\lim _(h\to0)((-2xh-h^2)/(h))`

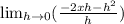
Factor out the greatest common factor h.

`\lim _(h\to0)(h(-2x-h))/(h)=\lim _(h\to0)(-2x-h)`

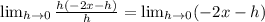
At last, evaluate the expression when h = 0.

`\lim _(h\to0)(-2x-h)=-2x-0=-2x`

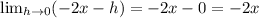
The slope is given by the equation -2x.

Let's evaluate the expression when x = 2 to find the value of the slope.

`m=-2x=-2(2)=-4`

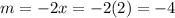
(a) Therefore, the slope is -4.

To find the equation for the tangent, we have to use the point-slope formula.

`\begin{gathered} y-y_1=m(x-x_1);\text{ where} \\ x_1=2,y_1=11,m=-4 \end{gathered}`

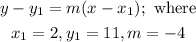
Use the values of the coordinates and slope to find the equation.

`\begin{gathered} y-11=-4(x-2) \\ y-11=-4x+8 \\ y=-4x+8+11 \\ y=-4x+19 \end{gathered}`

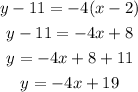
(b) Therefore, the equation for the tangent to the curve is y = -4x+19.

(c)

The image below shows the function f(x) and the tangent.