Answer:
30 x + 120y ≤ 480
10x + 9 y ≥ 72
Step-by-step explanation;
Here are Judy's requirements in a nutshell:
Additional Protein ≥ 72 grams
Additional Calories ≤ 480
Now, let us look at the protein and caloric value of Parmesan and Cheddar cheese.
For parmesan, 1 ounce has
10g protein
30 calories
Now if we have x ounces of parmesan, then the amounts they contain will be
10x grams protein
30x calories
For cheddar, 1 ounce has
9g protein
120 calories
Now if we have y ounces of cheddar, then the amounts they contain will be
9y grams protein
120y calories
Therefore, if I have x ounces of parmesan and y ounces of cheddar cheese, then Judy's protein requirement tells us that
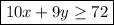
and her caloric requirement tells us that

Plotting these two inequalities gives