We have that the parent function of a quadratic graph is
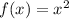
The graph of a quadratic graph is always a parabola
The parts of a parabola are
• Vertex
,
• Axis of symmetry
,
• Latus rectum
,
• Focus
,
• Directrix
,
• y-intercept
,
• x-intercept
The graph can be affected:
If we add a positive number to the x-variable, then the graph will move to the left.
If we add a negative number to the x-variable, then the graph will move to the right.
If we add a positive number to the function, then the graph will move upwards.
If we add a negative number to the function, then the graph will move downwards.
If we multiply -1 to the x- variable we will have a reflection over the y-axis
If we multiply -1 to the function we will have a reflection over the x-axis
if we multiply a number between 0 and 1 to the x-variable we will have a horizontal stretch
if we multiply a number greater than 1 to the x- variable we will have a horizontal compression
if we multiply a number between 0 and 1 to the function we will have a vertical compression
if we multiply a number greater than 1 to the function we will have a vertical stretch