Given the following system of equations:
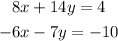
we can solve for 'x' the first equation to get the following:
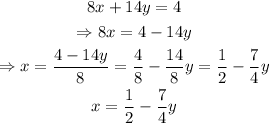
now that we have an expression for 'x', we can substitute it on the second equation to get:
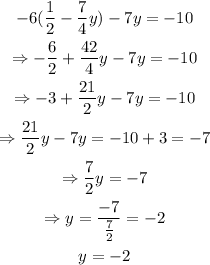
we have that y = -2, now we can use this value to find 'x':
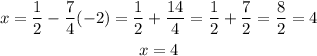
therefore, the solution of the system using substitution is (4,-2)