Question

The expression a^3 · a^5/ a^-1 can be written as a^n. what is the value of n?

Answer 1

n=9

Step-by-step explanation:

Given the expression

`a^3\cdot(a^5)/(a^(-1))`

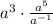
First, we apply the subtraction law of indices (to divide powers with the same base, subtract the indices) to the quotient to obtain:

`\begin{gathered} =a^3\cdot a^(5-(-1)) \\ =a^3\cdot a^(5+1) \\ =a^3\cdot a^6 \end{gathered}`

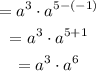
Next, we apply the addition law of indices (to multiply powers with the same base, add the indices).

`\begin{gathered} =a^(3+6) \\ =a^9 \end{gathered}`

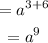
The value of n in a^n is therefore 9.