We will solve as follows:
*
We first determine the slope of AB, that is:
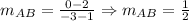
And using the properties of perpendicular lines, we have the following:
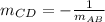
Where mCD is the slope of the points C & D, therefore:
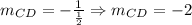
So, now we find the slope of CD using its coordinates, that is:
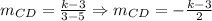
Now, we equal both values of mCD:
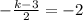
Now, we solve for k:

So, the points such that AB is perpendicular to CD are A(1,2), B(-3, 0), C(5, 3) & D(3, 5).
k = 7.
**
We determine the slope of BC:
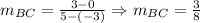
From this, we have that the slope of AD is:

And now, we calculate the slope of AD using its coordinates, that is:
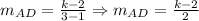
Now, we equal both values of the slope of AD, that is:
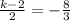
Now, we solve for k:
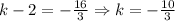
So, we have that the points such that AD is perpendicular to BC are A(1, 2), B(-3, 0), C(5, 3) & D(3, -10/3).
k = -10/3.