1 Answer

Deepak Kumar T P · Answer 1 · 2023-01-08T02:16:12+0000

Step-by-step explanation

The shaded area represents a segment. This can be solved with the formula below;

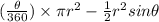
$\mleft((\theta)/(360)\mright)*\pi r^2-(1)/(2)r^2sin\theta$

Since the triangle is an equilateral triangle, it implies that the angle subtended at the centre is 60 degrees. Also, the given radius is 7 cm

$\begin{gathered} =7^2((60)/(360)*3.14-(1)/(2)*\sin 60)^{}_{} \\ =49((3.14)/(6)-\frac{\sqrt[]{3}}{4}) \\ =4.43\operatorname{cm}^2 \end{gathered}$

Answer:

$4..43\operatorname{cm}^2$

Please log in or register to add a comment.