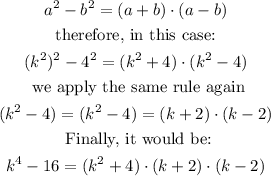Question

What method could work with four terms?k^4 - 16Simplify

Answer 1

The method would be the difference of squares

`k^4-16=(k^2+4)\cdot(k+2)\cdot(k-2)`

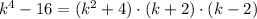
Explanation:

We have the following expression:

`k^4-16`

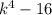
The first thing is to apply the law of exponents, like this:

`\begin{gathered} x^(a\cdot b)=(x^{a^{}})^b \\ \text{therefore:} \\ (k^2)^2-16 \\ \text{ we also know that:} \\ 16=4^2 \\ \text{replacing} \\ (k^2)^2-4^2 \end{gathered}`

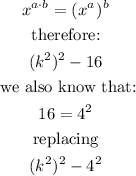
Now, we apply the rule of binomial square subtraction (Difference of squares), like this:

`\begin{gathered} a^2-b^2=(a+b)\cdot(a-b) \\ \text{therefore, in this case:} \\ (k^2)^2-4^2=(k^2+4)\cdot(k^2-4) \\ \text{ we apply the same rule again} \\ (k^2-4)=(k^2-4)=(k+2)\cdot(k-2) \\ \text{ Finally, it would be:} \\ k^4-16=(k^2+4)\cdot(k+2)\cdot(k-2) \end{gathered}`