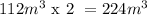The figure is a cuboid.
The volume of a cuboid is given by
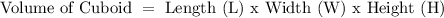
So, the volume of a cuboid is basically multiplying out all the sides.
Let us identify the sides of the cuboid,
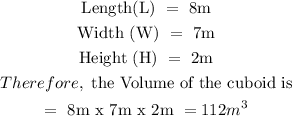
If two boxes(cuboids) are stacked on top of each other,
then the volume would be