Question

I wanted to know how to solve it and answers

Answer 1

we know that

The circumference is

70.000 ± 0.500

so

C=70.500 or C=69.500

step 1

Find out the radius of the sphere

`C=2\pi r`

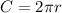
For C=70.500

`\begin{gathered} 70.500=2\pi r \\ r=(70.500)/(2\pi) \\ r=11.220 \end{gathered}`

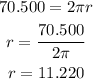
For C=70.000

`\begin{gathered} 70.000=2\pi r \\ r=(70.000)/(2\pi) \\ \\ r=11.141 \end{gathered}`

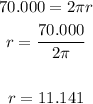
step 2

Find out the surface area

For r=11.220

`\begin{gathered} SA=4\pi r^2 \\ SA=4\pi((70.50)/(2\pi))^2 \\ SA=1,582.882 \end{gathered}`

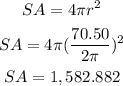
For r=11.141

`\begin{gathered} SA=4\pi((70.000)/(2\pi))^2 \\ SA=1,560.510 \end{gathered}`

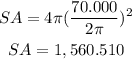
The maximum error is given by the difference

1,582.882-1,560.510=22.372