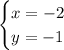Solving a system of linear equations by the graphical method consists of representing the equations of the system and the solution of this is the point of intersection between the graphs.
Since a single line passes through 2 points, then to graph the first equation, you can give two arbitrary values to x, replace them in the equation and find their respective y-coordinates.
So if for example, you take x = 1 and x = 2, you have

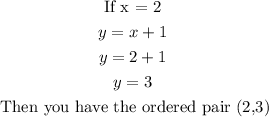
Graph the ordered pairs found and join them to obtain the graph of the first equation:
Now do the same with the second equation. If for example, you take x = 0 and x = -1, you have


Graph the ordered pairs found and join them to obtain the graph of the second equation:
Finally, as you can see the graphs of the equations intersect in the ordered pair (-2, -1), therefore the solution of the given system of equations is