ANSWER
6.15 · 10⁸ kg
Step-by-step explanation
Given:
• The force of attraction between the two tankers, F = 3.5x10³N
,
• The distance between their centers of mass, r = 85m
,
• The two tankers have equal masses, m₁ = m₂ = m
Known:
• The gravitational constant, G = 6.67 x 10⁻¹¹ Nm²/kg²
Unknown
• The mass of each tanker, m
By Newton's law of universal gravitation, we have that the force of attraction between two objects of masses, m₁, and m₂, separated by a distance r is,
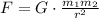
In this case, both masses are equal,
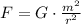
Solving for m,
![m=r\sqrt[]{(F)/(G)}](https://img.qammunity.org/2023/formulas/physics/high-school/2i61x770oi81dd7qn9ano0sethdwx9zo8r.png)
Replace with the values,
![m=85m\cdot\sqrt[]{\frac{3.5*10^3N}{6.67*10^(-11)Nm^2/\operatorname{kg}}}\approx6.15*10^8\operatorname{kg}]()