We have a triangle with perimeter P = 65ft and sides:
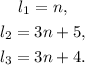
The perimeter of a geometrical figure is just the sum of the sides. In this case, we have:
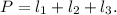
Replacing the data of the problem, we have:

Solving for n the last equation, we get:
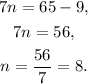
Replacing the value n = 8 in the equations for each side, we get:

Answer
The lengths of the sides are 8ft, 29ft and 28ft.