To graph lineal inequalities:
1. Solve in the inequality the variable y:
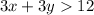
- Substract 3x in both sides of the inequation:
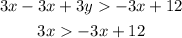
- Divide both sides of the inequation into 3:
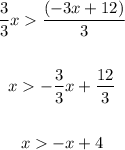
2. Find two points in the line that limits the inequality
The line is y=-x+4
Find y when x=0
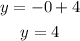
Find x when y=0:
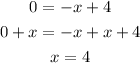
You have the next two points in the line: (0,4) and (4,0)
3. Put the points in the plane and draw the line that passes trought those points:
When the inequality is < or > you draw a dotted line (the line is not part of the solution)
When the inequality is ≥ or ≤ you draw a line (it is part of the solution)
4. Shadow the area that correspond to the inequality:
When the inequality is < or ≤ you shadow the area under the line
When the inequality is > or ≥ you shadow the area over the line.
In this case as the inequality symbol is > you draw a dotted line and shadow the area over the line. You get the next graph: