The Solution:
given the derivative function below:
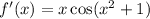
We are required to find the number of points of inflection of the graph of the function f(x) on the open interval -2 < x < 2
Recall:
At the point of inflection of a function, the second derivative of the function is equal to zero. That is,
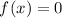
Differentiating f'(x) with respect to x using the Product Rule, we get

Where:
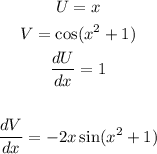
Substituting, we get
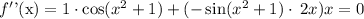
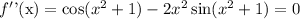
To find the number of points of inflection of the function, we shall solve graphically for x .
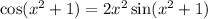
Solving graphically using the Desmos App, we have
From the graph, the points of inflection in the open interval - 2 < x < 2 exist at the points below:
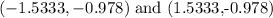
Thus, the number of points of inflection of the function in the given interval is 2.
Therefore, the correct answer is two (2).