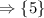1 Answer

Ask a Question

Pqvst · Answer 1 · 2023-08-18T08:55:07+0000

Answer:

The equation is given below as

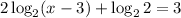
$2\log_2(x-3)+\log_22=3$

Step 1:

Apply the logarithm law of exponents below

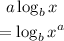
$\begin{gathered} a\log_bx \\ =\log_bx^a \end{gathered}$
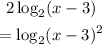
$\begin{gathered} 2\log_2(x-3) \\ =\log_2(x-3)^2 \end{gathered}$
$\begin{gathered} 2\operatorname{\log}_2(x-3)+\operatorname{\log}_22=3 \\ \log_2(x-3)^2+\operatorname{\log}_22=3 \end{gathered}$

Step 2:

Apply the logarithm law of addition below

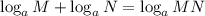
$\log_aM+\log_aN=\log_aMN$

By applying the law, we will have

$\begin{gathered} \operatorname{\log}_2(x-3)^2+\log_22=3 \\ \log_22(x-3)^2=3 \end{gathered}$

Step 3:

Apply the logarithm principle below

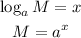
$\begin{gathered} \log_aM=x \\ M=a^x \end{gathered}$

By applying the principle, we will have

$\begin{gathered} \operatorname{\log}_22(x-3)^2=3 \\ 2(x-3)^2=2^3 \\ 2(x-3)^2=8 \\ divide\text{ both sides by 2} \\ (2(x-3)^2)/(2)=(8)/(2) \\ (x-3)^2=4 \end{gathered}$

Step 4:

Square root both sides and then add 3 to both sides

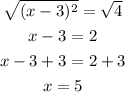
$\begin{gathered} √((x-3)^2)=√(4) \\ x-3=2 \\ x-3+3=2+3 \\ x=5 \end{gathered}$

Hence,

The solution set is

$\Rightarrow\lbrace5\rbrace$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions