Question

How do I know if it’s true or false for number 1?

Answer 1

We want to know if the following statements are true or false

item a)

`1-\cos x=\sin x`

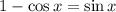
To solve this one, we're going to use the following identity

`\sin ^2x+\cos ^2x=1`

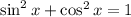
Rewriting this expression "isolating" the sine, we have

`\begin{gathered} \sin ^2x+\cos ^2x=1 \\ \sin ^2x=1-\cos ^2x \\ \sin x=\pm\sqrt[]{1-\cos^2x} \end{gathered}`

Using this in our expression, we have

`\begin{gathered} 1-\cos x=\sin x \\ \Rightarrow1-\cos x=\sqrt[]{1-\cos^2x} \end{gathered}`

When we have a difference of two squares, we can separate them as

`a^2-b^2=(a+b)(a-b)`

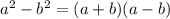
Using this in the argument of the square root, we have

`1-\cos ^2x=(1+\cos x)(1-\cos x)`

Using this to rewrite our expression

`\begin{gathered} 1-\cos x=\sqrt[]{1-\cos^2x} \\ 1-\cos x=\sqrt[]{(1+\cos x)(1-\cos x)} \\ 1-\cos x=\sqrt[]{(1+\cos x)}\sqrt[]{(1-\cos x)} \\ \frac{1-\cos x}{\sqrt[]{1-\cos x}}=\sqrt[]{1+\cos x} \end{gathered}`

We can rewrite the numerator of the left side of the equation as the product of its square root.

`1-\cos x=(\sqrt[]{1-\cos x})^2`

Using this in our expression, we have

`\begin{gathered} \frac{(\sqrt[]{1-\cos x})^2}{\sqrt[]{1-\cos x}}=\sqrt[]{1+\cos x} \\ \sqrt[]{1-\cos x}=\sqrt[]{1+\cos x} \\ 1-\cos x=1+\cos x \\ -\cos x=\cos x \end{gathered}`

Since the cosine of an angle is not equal to minus its value, the first statemente is FALSE.

item b)

`1-\cos ^2x=\sin ^2x`

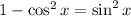
We're going to use the same identity to solve this one.

`\sin ^2x+\cos ^2x=1`

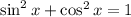
If we substitute the number 1 in our statement for this identity, we're going to have

`\begin{gathered} 1-\cos ^2x=\sin ^2x \\ (\sin ^2x+\cos ^2x)-\cos ^2x=\sin ^2x \\ \sin ^2x+\cos ^2x-\cos ^2x=\sin ^2x \\ \sin ^2x=\sin ^2x \\ 1=1 \end{gathered}`

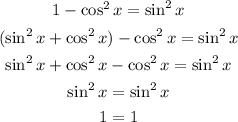
Since we got a true equation in the end, the statement on this item is TRUE.

item c)

`(1)/(\sin x)=\csc x`

This is a given identity(you can check it is a part of the table above the question), then, it is TRUE.

item d)

`(\cos x)/(\sin x)=\cos x((1)/(\sin x))`

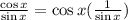
To solve this one, we're going to use the following property.

`(a)/(b)=a\cdot(1)/(b)`

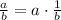
You can take out the numerator as a coefficient for our fraction.

Then, this statement is also TRUE.

item e)

`(\cos x)/(\sin x)=\cos x\csc x`

Using the previous two statements, we can solve this one,

Since the statement d is true

`(\cos x)/(\sin x)=\cos x((1)/(\sin x))`

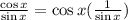
And statement c is also true

`(1)/(\sin x)=\csc x`

Then, if we substitute c on d, we have statement e, therefore, statement e is also TRUE.

item f)

`\cos ^2x-1=\sin ^2x`

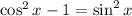
To solve this one, we're going to use the following identity

`\cos ^2x+\sin ^2x=1`

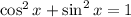
Again, making a substitution, we have

`\begin{gathered} \cos ^2x-1=\sin ^2x \\ \cos ^2x-(\sin ^2x+\cos ^2x)=\sin ^2x \\ \cos ^2x-\sin ^2x-\cos ^2x=\sin ^2x \\ -\sin ^2x=\sin ^2x \end{gathered}`

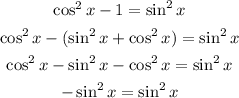
Since the last equation is false, then the statement f is also FALSE.

item g)

`(2)/(\cos x)=2\sec x`

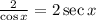
Using the same property used on item d, we have

`(2)/(\cos x)=2((1)/(\cos x))`

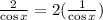
And also using the definition os sec x, we have

`\sec x=(1)/(\cos x)`

Using those properties in our statement, we have

`\begin{gathered} (2)/(\cos x)=2\sec x \\ 2((1)/(\cos x))=2\sec x \\ 2(\sec x)=2\sec x \\ 2\sec x=2\sec x \end{gathered}`

Then, our last statement g is also TRUE.