Question

A 2kg ball is swinging on a 1m string attached to the ceiling. At the bottom of the arc, its speed is 3m/s.What is the tension in the string at this point?

Answer 1

37.6 N

Step-by-step explanation:

We can represent the situation with the following

Then, the net force is equal to:

`\begin{gathered} F_(net)=T-mg=ma_c \\ \Rightarrow T-mg=m(v^2)/(r) \end{gathered}`

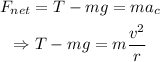
Where T is the tension, mg is the weight, m is the mass, v is the speed, and r is the radius of the circular motion of the ball. Solving for T, we get:

`T=m(v^2)/(r)+mg`

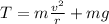
Now, we can replacing m = 2 kg, v = 3 m/s, r = 1 m, and g = 9.8 m/s²

`\begin{gathered} T=2((3^2)/(1))+2(9.8) \\ T=2(9)+19.6 \\ T=18+19.6 \\ T=37.6 \end{gathered}`

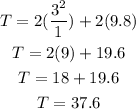
Therefore, the tension in the string at this point is 37.6 N