Step 1:
Write the equation
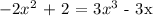
Step 2:
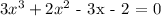
Next, find the first zero by trial and error. choose value of x that when you substitute will result in zero.
x = -1 will result into zero
Let check
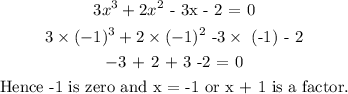
Step 4
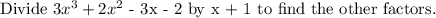
![\begin{gathered} \text{ 3x}^2\text{ - x -2} \\ \text{ x+ 1 }\sqrt[]{3x^3+2x^2\text{ - 3x - 2 }} \\ \text{ -(3x}^3+3x^2)\text{ } \\ \text{ -x}^2\text{ - 3x - 2} \\ \text{ -(-x}^2\text{ - x)} \\ \text{ -2x - 2} \\ \text{ -2x - 2} \\ \text{ 0} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ifdggt6116ie4f7cvjjlogrxod9fsyykk2.png)
Step 5:
Hence
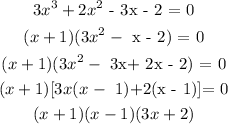
Final answer
Equate each factor to zero to find the values of x.
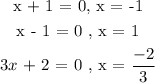
x = -1 , x = 1, x = -2/3