Question

Use the quadratic formula to solve for X9x^2 - 3x -1 = 0

Answer 1

x = -0.21, 0.54

Step-by-step explanation:

The quadratic formula says that if we have a quadratic equation of the form

`ax^2+bx+c=0^{}`

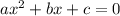
then the value of x is given by

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Now in our case, we have

`9x^2-3x-1=0`

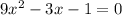
therefore, for the quadratic formula we put a = 9, b = -3, and c = -1 to get

`x=\frac{3\pm\sqrt[]{3^2-4(9)(-1)}}{2(9)}`

which simplifies to give

`x=\frac{3\pm3\sqrt[]{5}}{18}`
`\begin{gathered} x=(1)/(6)-\frac{\sqrt[]{5}}{6}\approx-0.21 \\ x=(1)/(6)+\frac{\sqrt[]{5}}{6}\approx0.54 \end{gathered}`

Hence, rounded to the nearest hundreth, the solutions to the quadratic equation are

x = -0.21 and x = 0.54.