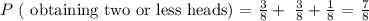SOLUTION:
Step 1:
In this question, we are given the following:
Step 2:
A.) State the random variable:
X= the number of heads observed when you flip a coin three times
Step 3:
B.) construct a probability distribution table for the number of heads obtained over three tosses. Enter the X values from smallest to largest:
X P(X)
0 1/8
1 3/8
2 3/8
3 1/8
Step 4:
C.) Determine the shape of the probability distribution of x
- symmetric
Step 5:
D.) find the MEAN number of heads for this distribution
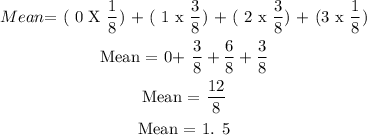
Step 6:
E.) find the standard deviation for the number of heads for this distribution:
![S\tan dard\text{ Deviation = }\sqrt[]{(x\text{ -}\mu)^2\text{ P ( X = x )}}](https://img.qammunity.org/2023/formulas/mathematics/college/4xrad5k29wbajvrqqpw63ahuza19s4ght4.png)
![\begin{gathered} \sin ce\text{ }\mu\text{ = 1. 5, then we have that:} \\ \sqrt[]{\lbrack(0-1.5)^2X\text{ }(1)/(8)\rbrack+\lbrack(1\text{ - }1.5)^2\text{X }(3)/(8)\rbrack+\lbrack(2-1.5)^2}X(3)/(8)\rbrack+\lbrack(3-1.5)^2\text{ X }(1)/(8) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/74kaj9n48swqhrddsb69cjv7f3ma1lsrre.png)
![\begin{gathered} \sqrt[]{(2.\text{ 25 X }(1)/(8))\text{ + ( 0.25 X }(3)/(8))\text{ + ( 0. 25 X }(3)/(8))\text{ + (2.25 X }(1)/(8))} \\ =\text{ }\sqrt[]{0.28125+\text{ 0.09375 + 0.09375 + 0.28125}} \\ =\sqrt[]{0.75} \\ =0.866\text{ ( 3 decimal places)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/e799ij357yn2ly0bollpdttv32m43eme1p.png)
Step 7:
F.) find the probability of obtaining two or less heads over three tosses of a coin