Question

a nut is shaped like a regular hexagon. this nut has side lengths of 2 centimeters. find x. (round to the nearest tenth)

Answer 1

Step 1 :

We are meant to find the side x, ( round to the nearest tenth ).

We have the nut has side lengths of 2 cm and the nut is shaped like a regular hexagon.

Step 2 :

We also need to find the internal angle of a hexagon,

`\begin{gathered} =(n-2)X180^0^{} \\ \text{where n = 6 } \\ =(6-2)X180^0^{} \\ =\text{ }4X180^0 \\ =720^0 \\ \end{gathered}`

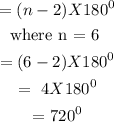
Each internal angle =

`(720^0)/(6)=120^{0\text{ }}`

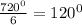
Step 3 :

To get x, we need to do the following :

`\begin{gathered} x=(2sin60^{0\text{ }})\text{ + ( 2sin}60^0\text{ )} \\ x=4sin60^0 \\ x\text{ = 4 x 0.8660} \\ x\text{ = 3. 464 cm} \\ x\text{ = 3. 5 cm ( to the nearest tenth )} \end{gathered}`

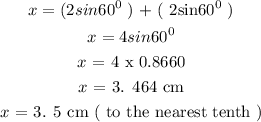
CONCLUSION :

The value of x = 3. 5 cm ( to the nearest tenth )