Question

Four wires running through the corners of a square with sides of length 14.913 cm carry equal currents, 2.338 A. Calculate the magnetic field at the center of the square.

Answer 1

We know that the magnitude of the magnetic field due to a current if given by:

`\begin{gathered} B=(\mu_0I)/(2\pi r) \\ \text{ where:} \\ \mu_0=4\pi*10^(-7)\text{ }(H)/(m) \\ I\text{ is the current} \\ r\text{ is the distance to the point of interest } \end{gathered}`

To help us calculate the distance we can draw a square:

To find the distance r we need to notice that we have a right triangle, applying the pythagorean theore, we have:

`\begin{gathered} r=\sqrt{((0.14913)/(2))^2+((0.14913)/(2))^2} \\ r=√((0.074565)^2+(0.074565)^2) \\ r=0.074565√(2) \end{gathered}`

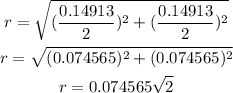
This means that the magnitude of the field due to each wire is:

`\begin{gathered} B=((4\pi*10^(-7))(2.338))/((2\pi)(0.074565)) \\ B=4.43*10^(-6) \end{gathered}`

Now, we need to remember that the magnetic field is a vector, assuming the currents point out of the page and using the right hand rule we have that the direction of each field is given by:

From the diagram we notice that the line fields cancel with each other; let's prove it:

`\begin{gathered} \vec{B}=<4.43*10^(-6)\cos45,4.43*10^(-6)\sin45>+<-4.43*10^(-6)\cos45,4.43*10^(-6)\sin45> \\ +<-4.43*10^(-6)\cos45,-4.43*10^(-6)\sin45>+<4.43*10^(-6)\cos45,-4.43*10^(-6)\sin45> \\ =<0,0> \end{gathered}`

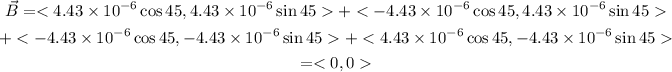
Therefore, the field at the center of the square is zero.

Note: We could have conclude the same by symmetry considerations but we prove it here so it is clearer.