Answer:
Step-by-step explanation:
Given:
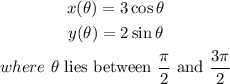
To find:
The graph of the parametric equations
When theta = pi/2, we'll have;
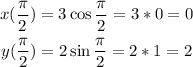
When theta = 3pi/4;
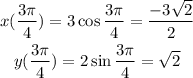
When theta = pi;

When theta = 5pi/4;

When theta = 3pi/2;
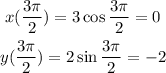
We can now go ahead and sketch the graph as seen below;