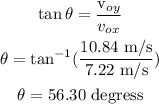Question

. A circus performer is shot out of acannon on the ground and needs to hit apaper target that is placed 8.0 mhorizontally away from the cannon and6.0 m above the ground. The performerneeds to hit the target at the peak of histrajectory. At what initial speed and at whatangle relative to the ground should theperformer be shot out of the cannon?

Answer 1

Given

x: Horizontal distance

x = 8 m

y: vertical distance

y = 11 m

Hit the target at the peak of the trajectory

Procedure

Let's first make a diagram of the situation.

Projectile Motion

Parabolic motions can be analyzed as the superposition of a horizontal motion and a vertical motion. Let's first analyze the vertical movement, which is very similar to free fall. Recall that the maximum point of the velocity at y is equal to 0 and from here we can calculate the y-component of the velocity.

`\begin{gathered} v^2_(fy)=v^2_(oy)-2gy \\ 0=v^2_(oy)-2gy \\ v_(oy)=\sqrt[]{2\cdot g\cdot y}_{} \\ v_(oy)=\sqrt[]{2\cdot9.8\cdot6} \\ v_(oy)=10.84\text{ m/s} \end{gathered}`

Now we can calculate the time it takes to go to the maximum point.

`\begin{gathered} v_(fy)=v_(oy)-gt \\ 0=v_(oy)-gt \\ t=(v_(oy))/(g) \\ t=\frac{10.84\text{ m/s}}{9.8m/s^2} \\ t=1.10\text{ s} \end{gathered}`

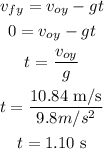
Finally we can calculate the velocity in x

`\begin{gathered} v_(ox)=(x)/(t) \\ v_(ox)=(8m)/(1.10s) \\ v_(ox)=7.23\text{ m/s} \end{gathered}`

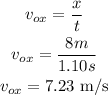
We have the x and y components of the initial velocity. Now we can calculate the magnitude and the angle.

`\begin{gathered} v^2_o=v^2_(ox)+v^2_(oy) \\ v_o=\sqrt[]{10.84^2+7.22^2} \\ v_o=13.03\text{ m/s} \end{gathered}`
`\begin{gathered} \tan \theta=\frac{\text{v}_(oy)}{v_(ox)} \\ \theta=\tan ^(-1)(\frac{10.84\text{ m/s}}{7.22\text{ m/s}}) \\ \theta=56.30\text{ degress} \end{gathered}`