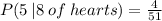![undefined]()
1) Since there are four cards 8 (hearts-clubs- diamonds and spades) in a deck of cards we proceed.
a) Note that, this is Conditional Probability, so let's do it:
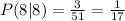
Note that this is because we needed to find the probability of taking and eight given that an 8 has been drawn. So there were only three 8-cards out of 51
b) Now, let's work with the chance of the second card being another heart given that the 8 of hearts has been already drawn:
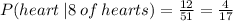
Note that there are 13 hearts, but once has already gone, so we can tell
c) Similarly to the previous one, let's find the probability that the second card is club given that the first one was an 8 of hearts.
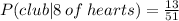
Note that there were 13 club of hearts left and 51 as a total number.
d) Now, let's do it for the probability of this second card being a 5 given that an 8 of cards has gone: