When two triangles are similar, the ratio between their corresponding sides is equal to a constant(the scale factor between the triangles). The original triangles in our problem have a scale factor of 3:
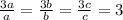
If we add 6 to the sides of both triangles, this is no longer true. We can't rewrite the ratio between the corresponding sides as a constant:
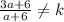
therefore, the triangles wouldn't be similar.