Question

The slope of the linear function y = 5/4x + 1/2 is changed to where 5/8, where y = 5/8x + 1/2 Identify the transformation required to produce the new slope, state the equation of the transformed function, and explain what the graph of the transformedline looks like.

Answer 1

Horizontal stretch

see explanation below

Step-by-step explanation:

Initial linear function: y = 5/4x + 1/2

slope = 5/4

The new linear function: y = 5/8x + 1/2

slope = 5/8

5/8 ÷ 5/4 = 5/8 × 4/5 = 1/2

We say the transformation is an horizontal stretch as the x axis of the function is transformed.

If f(x) is 5/4 x and g(x) is the new linear function:

`g(x)\text{ = f(}(1)/(2)x)\text{ + 1/2}`

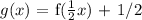
I plotted both graph so it would be easy to compare

plotting the graph for the first linear function:

plotting the graph for the 2nd linear function: