Question

Suppose that the duration of a particular type of criminal trial is known to be normally distributed with a mean of 17 days and a standard deviation of 4 days. Let X be the number of days for a randomly selected trial. Round all answers to 4 decimal places where possible.b. If one of the trials is randomly chosen, find the probability that it lasted at least 18 days.

Answer 1

We know that the distribution is normal with mean 17 and standard deviation 4; in this case we need to find:

`P(X\ge18)`

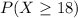
Using the properties of the binomial distribution this is equal to:

`P(X\ge18)=1-P(X\leq18)`

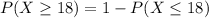
To find the probability on the right we will standardize the distribution, then we need the z-score which is given by:

`z=(x-\mu)/(\sigma)`

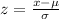
Then we have:

`\begin{gathered} P(X\geqslant18)=1-P(X\leqslant18) \\ =1-P(X\leq(18-17)/(4)) \\ =1-P(X\leq0.25) \end{gathered}`

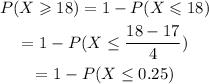
Using a standard normal distribution table we have:

`\begin{gathered} P(X\geqslant18)=1-P(X\leqslant18) \\ =1-P(X\leq(18-17)/(4)) \\ =1-P(X\leq0.25) \\ =1-0.5987 \\ =0.4013 \end{gathered}`

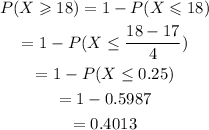
Therefore, the probability that the trial lasts at least 18 days is 0.4013