To solve this problem, we will use the following properties
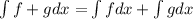
(The integral of the sum is the sum of the integrals).
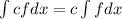
(The integral of a constant times a function is constant times the integral of the function)
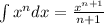
only when n is not -1.
First, recall that
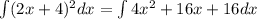
using the sum property, we have
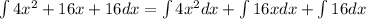
Now, we will solve each integral apart. We will use the last two properties to do so.
Note that
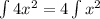
we identify that in this case, the function is of the form x^n where n=2. Then, using the last property we get
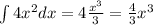
Also, note that
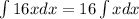
we identify that the function is of the form x^n where n=1. Then,
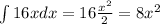
Finally, we have
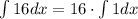
we note that 1=x⁰. So we have
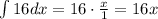
Then, by adding all results we get
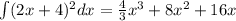
Since we are finding the function whose derivative is (2x+4)², we add a constant C. So we have
