Question

In an arithmetic sequence, if the 4th term is 3 and the 22nd term is 15, then what is the 1st term?2/31-3-4/3None of the above

Answer 1

Answer:

The 1st term = 1

Explanations:

The nth term of an arithmetic sequence is given by the formula:

`T_n=\text{ a + (n-1)d}`

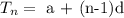
The fourth term will therefore be:

`\begin{gathered} T_4=\text{ a + (4-1)d} \\ T_4=\text{ a + 3d} \end{gathered}`

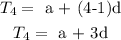
The fourth term is 3

`\begin{gathered} T_4\text{ = }3 \\ a\text{ + 3d = 3}\ldots\ldots\ldots...\ldots\text{...}(1) \end{gathered}`

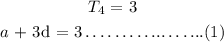
The 22nd term will be given by the formula:

`\begin{gathered} T_(22)=\text{ a + (22-1)d} \\ T_(22)\text{ = a + 21d} \end{gathered}`

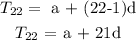
The 22nd term is 15

`\begin{gathered} T_(22)=\text{ 15} \\ a\text{ + 21d = 15}\ldots\ldots\ldots\ldots.(2) \end{gathered}`

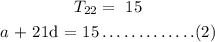
Subtract equation (1) from equation (2)

18d = 12

d = 12/18

d = 2/3

Substitute d = 2/3 into equation (1)

`\begin{gathered} a\text{ + 3(}(2)/(3))\text{ = 3} \\ a\text{ + 2 = 3} \\ a\text{ = 3 - 2} \\ a\text{ = 1} \end{gathered}`

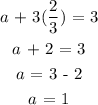
Since a represent the 1st term

The first term = 1