• mean = 79.8
,
• mean = 14.4
1) Solving for m, plugging it for the z-score formula we have:
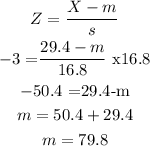
We can state then the mean is 79.8, the s stands for Sample Deviation. Note that we multiplied both sides by 16.8 and added 50.4 to both sides
2) The second Z-score formula presents the following data:
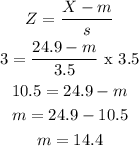
The difference for that is the Standard Deviation (3) and the Z-score.
3) Hence, the answer is
0. mean = 79.8
,
1. mean = 14.4