Question

If plane x averages 800 mph and plane y averages 400 mph how many hours will plane x travel before it overtakes plane y if plane y has a 2 hour and 30 min head start

Answer 1

2h 30min

Step-by-step explanation

The average speed of an object is:

`v=(\Delta x)/(\Delta t)`

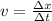
We know that plane x's speed is 800mph and plane y's is 400mph. We want to find at what time they will be in the same position:

`\Delta x=v\cdot\Delta t`

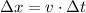
So we have to solve:

`\begin{gathered} \Delta x_X=\Delta x_Y \\ v_X\cdot\Delta t_X=v_Y\cdot\Delta t_Y \end{gathered}`

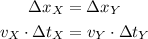
Remember that plane y had a 2.5 hour head start, so time between these two planes is:

`\Delta t_Y=\Delta t_X+2.5h`

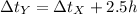
To simplify the equation, let's call Δt_X = t. So the equation to solve is:

`\begin{gathered} v_X\cdot t=v_Y\cdot(t+2.5h) \\ 800\text{mph}\cdot t=400\text{mph}\cdot(t+2.5h) \end{gathered}`

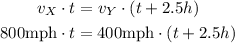
First apply distributive property on the right side of the equation:

`\begin{gathered} 800\cdot t=400\cdot t+400\cdot2.5 \\ 800\cdot t=400\cdot t+1000 \end{gathered}`

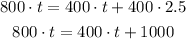
Subtract 400t from both sides of the equation:

`\begin{gathered} 800t-400t=400t-400t+1000 \\ 400t=1000 \end{gathered}`

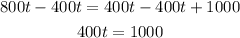
And divide both sides by 400:

`\begin{gathered} 400\cdot(t)/(400)=(1000)/(400) \\ t=2.5 \end{gathered}`

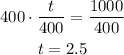
So the time it will take for plane x to overtake plane y is another 2 hours and 30 minutes