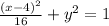Question

Running an equation of an eclipse given the center an endpoint of an axis and the length of the other axis

Answer 1

For this problem, we are given the characteristics of an ellipse, and we need to determine its expression.

The general expression for an ellipse is given below:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

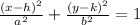
Where (h,k) are the coordinates of the center, a is the major radius and b is the minor radius.

We are given the length of the major axis, we need to divide it by 2 in order to find the major radius:

`a=(8)/(2)=4`

Then we are given the endpoint for the minor axis, which is (4, -1). Since this is aligned with the center at (4,0) we can determine the minor radius by subtracting the y-coordinates:

`b=0-(-1)=1`

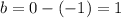
The ellipse's expression is:

`((x-4)^2)/(16)+y^2=1`