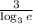Question

Change to base 3 and simplify:ln3 + ln9So confused! It says the answer is not 3ln3 nor ln27. Tried changing to logarithm but still stuck.

Answer 1

Given the expression:

`\ln 3+\ln 9`

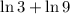
the given logarithms are written to the base (e), we will change the base to 3

First, we will simplify the expression then change the base to 3

As we know: ln(AB) = ln A + ln B

so, the given expression can be written as:

`\ln 3+\ln 9=\ln (3\cdot9)=\ln 27`

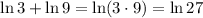
now, we will change (ln 27) from the base (e) to the base (3) as follows:

`\begin{gathered} y=\ln 27 \\ e^y=27 \end{gathered}`

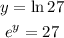
Now, taking the logarithm to the base 3

so,

`\begin{gathered} \log _3e^y=\log _327 \\ y\cdot\log _3e=\log _33^3 \\ y\cdot\log _3e=3\cdot\log _33 \\ y\cdot\log _3e=3\cdot1 \\ y\cdot\log _3e=3 \\ \\ y=(3)/(\log _3e) \end{gathered}`

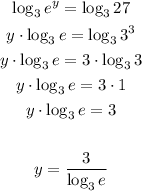
so, the answer will be:

`(3)/(\log _3e)`