Question

In a city with a population of 65,000 people the number of people p(t) exposed to a rumor in t hours is given by the function p(t)=65,000(1-e^-0.0009t) round your answers to the nearest hour.Find the number of hours until 20% of the population have heard the rumor.Find the number of hours until 60% of the population have heard the rumor.

Answer 1

Given:

`\begin{gathered} \text{The model } \\ p(t)=65,000(1-e^(-0.0009t)) \end{gathered}`

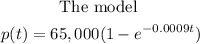
Where t = number of hours

We are required to find the number of hours until 20% and 60% of the population have heard the rumor.

(A) Find the number of hours until 20% of the population have heard the rumor:

20% of the population =

`\begin{gathered} (20)/(100)\text{ x total population} \\ =(20)/(100)\text{ x 65,000} \\ =13,000 \end{gathered}`
`\begin{gathered} \text{Substitute p(t) = 13000 into the model} \\ p(t)=65,000(1-e^(-0.0009t)) \\ 13,000=65,000(1-e^(-0.0009t)) \\ (13000)/(65000)=1-e^(-0.0009t) \\ 0.2=1-e^(-0.0009t) \\ 0.2-1=-e^(-0.0009t) \\ -0.8=-e^(-0.0009t) \\ e^(-0.0009t)=0.8 \\ \text{take ln of both sides} \\ \ln e^(-0.0009t)=\ln 0.8 \end{gathered}`
`\begin{gathered} -0.0009t\ln e=-0.22314 \\ -0.0009t(1)=-0.22314 \\ t=(-0.22314)/(-0.0009) \\ t=247.933 \\ t=248\text{ hours (nearest hour)} \end{gathered}`

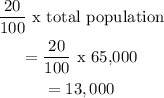
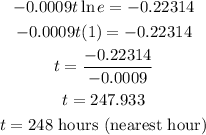
The number of hours until 20% of the population have heard the rumor is 248 hours

(b) Find the number of hours until 60% of the population have heard the rumor

60% of the population =

`\begin{gathered} (60)/(100)\text{ x 65000} \\ =39000 \end{gathered}`
`\begin{gathered} \text{Substitute p(t) =39000 into the model} \\ p(t)=65,000(1-e^(-0.0009t)) \\ 39000=65,000(1-e^(-0.0009t)) \\ \text{Divide both sides by 65000} \\ (39000)/(65000)=(65,000)/(65000)(1-e^(-0.0009t)) \\ \\ 0.6=1-e^(-0.0009t) \\ 0.6-1=-e^(-0.0009t) \\ -0.4=-e^(-0.0009t) \\ 0.4=e^(-0.0009t) \\ e^(-0.0009t)=0.4 \\ \text{take ln of both sides} \\ \ln e^(-0.0009t)=\ln 0.4 \\ -0.0009t\ln e=\ln 0.4 \\ -0.0009t(1)\text{ = -0.9162} \\ -0.0009t\text{= -0.9162} \\ t=(-0.9162)/(-0.0009) \\ t=1018.1 \\ t=1018hours\text{ (nearest hour)} \end{gathered}`

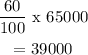
The number of hours until 60% of the population have heard the rumor is 1018 hours