Question

The following function represents the ending balance in a savings account that earns interest at theend of each year. Let t denote the year since the initial investment. B(t) = 3000 (1.05)^ t1) Is this function increasing or decreasing? Explain how you know.2) What is initial investment?3) What is the growth factor per year?4) What is the annual interest rate per year (as a percent)?

Answer 1

`B(t)=3000(1.05)^t`

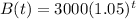
1) Given that the base of the exponent is 1.05, which is greater than 1, then the function is increasing

2) Substituting with t = 0 into the equation, we get:

`\begin{gathered} B(0)=3000(1.05)^0 \\ B(0)=3000\cdot1 \\ B(0)=3000 \end{gathered}`

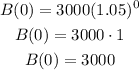
The initial investment is $3,000

3) The growth factor is the base of the exponential function, that is, 1.05

4) There are two ways to express an exponential function:

`\begin{gathered} f(t)=a\cdot b^t \\ Or \\ f\mleft(t\mright)=a\mleft(1+r\mright)^t \end{gathered}`

where:

`b=1+r`

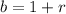
As stated before, the base is b = 1.05. In terms of variable r (the interest rate):

`\begin{gathered} 1.05=1+r \\ 1.05-1=1-1+r \\ 0.05=r \end{gathered}`

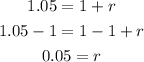
Expressing the interest rate as a percent:

`r=0.05\cdot100=5\text{ \%}`