The answer is constantly increasing (Option B)
The function f(x) is clearly increasing as the independent variable x increases, when x is greater than 0 i.e. when x is positive.
The unclear thing is whether or not f(x) is increasing or decreasing or constant when x is less than 0 i.e when x is negative.
Notice that f(x) can never be -1. This is because:
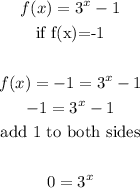
As we can see, the exponential expression equals zero if f(x) is -1. This is an impossible phenomenon and therefore the values for x are undefined when f(x) = - 1 .
Therefore, this gives us a basis for predicting what is actually going on the negative x-axis.
Because f(x) cannot be -1 (so that x doesn't become undefined), therefore, we can expect that the graph cannot touch the line f(x) = -1. This is exactly what we see in the graph itself.
So, as the graph moves from the positive x-axis into the negative x-axis, the values of f(x) approach -1 but continue that way ad infinitum.
Therefore we can conclude that because the values of f(x) approaches -1 as x moves from the positive axis to the negative axis (i.e. f(x) reduces infinitely), we can say that as x moves from left to right or from negative to positive, the values of f(x) which approach -1 on the negative x-axis, always increases.
The answer is constantly increasing (Option B)