Question

Find three consecutiveintegers with a sum of48.

Answer 1

First, we have to express algebraically the part "three consecutive integers".

`x,x+1,x+2`

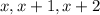
According to the problem, these three consecutive integers have to sum 48. So, we can express the following equation.

`x+x+1+x+2=48`

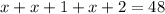
Now, we solve for x

`3x+3=48`

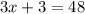
We subtract 3 on each side-

`\begin{gathered} 3x+3-3=48-3 \\ 3x=45 \end{gathered}`

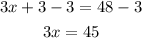
At last, we divide the equation by 3

`\begin{gathered} (3x)/(3)=(45)/(3) \\ x=15 \end{gathered}`

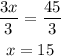
Therefore, the first number is 15, the second is 16 and the last number is 17.