Question

In the parallelogram below, if ∠∠A= 25° degrees, and ∠∠C= (5x + 5)°, find x.

Answer 1

Given:

• ∠A = 25 degrees

,

• ∠C = (5x + 5) degrees.

Let's find the value of x.

In a parallelogram, the opposite angles are congruent.

Angle A and angle C are opposite angles of the parallelogram, thus they are congruent angles.

Thus, we have:

`\begin{gathered} \angle A=\angle C \\ \\ 25=5x+5 \end{gathered}`

Let's solve for x in the equation,

Subtract 5 from both sides of the equation:

`\begin{gathered} 25-5=5x+5-5 \\ \\ 20=5x \end{gathered}`

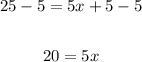
Divide both sides by 5:

`\begin{gathered} (20)/(5)=(5x)/(5) \\ \\ 4=x \\ \\ x=4 \end{gathered}`

Therefore, the value of x is 4 .

• ANSWER:

c. 4